Definición de logaritmo

El logaritmo en base \(b\) de un número \(a> 0\) se representa por \( \log_b (a)\) y es el número \(c\) que cumple \(b^c = a\):

$$ \log_b (a) = c \Leftrightarrow b^c = a $$

Nota: la base \(b\) debe ser un número real positivo distinto de 1. El número \(a\) recibe el nombre de argumento del logaritmo.

Ejemplos:

• El logaritmo en base \(10\) de \(1000\) es \(3\) porque \(10^3 = 1000\):

  $$ \log_{10}(1000) = 3$$

• El logaritmo en base \(5\) de \(125\) es \(3\) porque \(5^3 = 125\):

  $$ \log_{5}(125) = 3 $$

• El logaritmo en base \(10\) de \(1\) es \(0\) porque \(10^0 = 1\):

  $$ \log_{10}(1) = 0 $$

Logaritmo decimal

El logaritmo decimal es el logaritmo en base \(10\):

$$ \log_{10}(x)$$

Ejemplo: \(\log_{10}(1000) = 3 \).

Es habitual no indicar la base en el logaritmo decimal, pero nosotros lo haremos para evitar confusiones.

Gráfica:

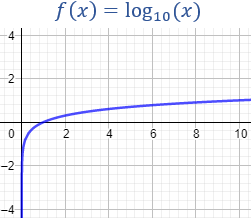
Observad de que se trata de una función que siempre crece: primero lo hace muy rápidamente (\(0< x \leq 1\)) y después muy lentamente (\(x \geq 1\)).

Logaritmo binario

El logaritmo binario es el logaritmo en base \(2\):

$$ \log_{2}(x)$$

Ejemplo:

\(\log_{2}(8) = 3 \)

Gráfica:

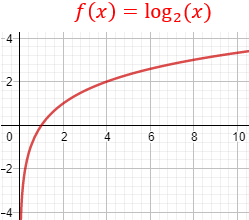
Observad que el compartamiento de la función es similar al del logaritmo decimal, pero el crecimiento es ahora menos exagerado: no crece tan rápidamente en \(0< x \leq 1\) y crece menos lentamente en \(x \geq 1\).

Logaritmo natural

El logaritmo natural es el logaritmo en base \(e\) (es decir, el número de Euler, \(e \approx 2,7182... \)):

$$ \log_{e}(x)$$

Normalmente, el logaritmo natural se escribe como

$$ \ln(x) $$

Ejemplo: \(\ln(e^3) = \log_{e}(e^3) = 3 \).

No es correcto llamar logaritmo neperiano al logaritmo en base \(e\) (logaritmo natural), aunque es muy habitual que se haga. El logaritmo neperiano lo veremos a continuación.

Gráfica:

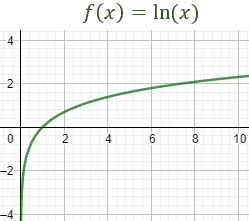
El comportamiento de la función es también similar al de los logaritmos anteriores.

Diferencias

El logaritmo natural está entre el decimal y el binario:

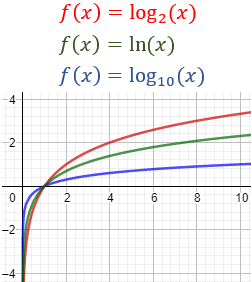
Observad que cuanto mayor es la base, más lento es el crecimiento de la función para \(x \geq 1\) y al contrario para \(0< x \leq 1\).

Los logaritmos son crecientes cuando su base es mayor que \(1\) y decrecientes cuando \(0 < b < 1\). Esto se deduce al cambiar la base del logaritmo a la decimal:

$$ \log_b(x) = \frac{\log_{10}(x)}{\log_{10}(b)} $$

Teniendo en cuenta que el logaritmo decimal es creciente y que el signo del denominador depende de si \(b\) es mayor o menor que \(1\), se deduce su monotonía.

Logaritmo neperiano

Este logaritmo difiere de los anteriores en que no tiene su propio nombre por tener una base concreta (como el decimal, binario o natural), sino porque se define como un cociente de logaritmos.

Su nombre es en honor al matemático escocés John Napier (1550-1617), que fue el primero que definió los logaritmos.

El logaritmo neperiano se define como sigue:

$$ NapLog(x)= \frac{ \log\left( \frac{10^7}{x}\right) }{ \log\left( \frac{10^7}{10^7-1}\right) } $$

Gráfica:

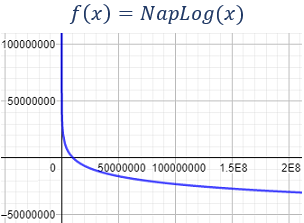
Observad que este logaritmo es decreciente.

Observad también la escala de la gráfica.

Aplicaciones

Para terminar, diremos que la importancia de los logaritmos se debe a sus múltiples y variadas aplicaciones en las matemáticas. Una de ellas es la resolución de ecuaciones exponenciales debido a sus propiedades. Por ejemplo, la solución de la ecuación \( 3^x = 5^{x+1} \) es

$$ x = \frac{\log(5)}{\log(3)-\log(5)} \approx -3.1507 $$

Aplicaciones destacadas:

• Ecuaciones logarítmicas

• Ecuaciones exponenciales

Ejercicio 1

Calculad los siguientes logaritmos decimales:

1. \( \log_{10}(1)\)

2. \( \log_{10}(100)\)

3. \( \log_{10} \left(\frac{1}{100}\right) \)

4. \( \log_{10}(0.1)\)

5. \( \log_{10}(0.001)\)

Solución:

Todos los argumentos son potencias de \(10\), así que el resultado del logaritmo es el exponente de su argumento:

1. \( \log_{10}(1)\)

   Como \(1 = 10^0\),

   $$ \log_{10}(1) = \log_{10}(10^0) = 0 $$

2. \( \log_{10}(100)\)

   El número \(100\) es la potencia \(10^2\) (el exponente es el número de ceros). Por tanto,

   $$ \log_{10}(100) = \log_{10}(10^2) = 2 $$

3. \( \log_{10} \left(\frac{1}{100}\right) \)

   Recordad que el exponente negativo es la inversa de una fracción. La fracción puede escribirse como una potencia de \(10\):

   $$ \frac{1}{100} = \frac{1}{10^2} = 10^{-2}$$

   Por tanto, el logaritmo es

   $$ \log_{10} \left(\frac{1}{100}\right) = \log_{10}(10^{-2}) = -2$$

4. \( \log_{10}(0.1)\)

   El número decimal \(0.1\) es la fracción \(1/10\), es decir, la potencia \(10^{-1}\). Por tanto,

   $$ \log_{10}(0.1) = \log_{10}(10^{-1}) = -1 $$

5. \( \log_{10}(0.001)\)

   El número decimal \( 0.001 \) es la potencia \(10^{-3}\) (el exponente es el número de ceros). Por tanto,

   $$ \log_{10}(0.001) = \log_{10}(10^{-3}) = -3 $$

Ejercicio 2

Calculad los siguientes logaritmos binarios:

1. \( \log_{2}(1)\)

2. \( \log_{2}(8)\)

3. \( \log_{2}\left(\frac{1}{32}\right) \)

4. \( \log_{2}(0.25)\)

5. \( \log_{2}(0.5)\)

Solución:

Todos los argumentos son potencias de \(2\), así que el resultado del logaritmo es el exponente de su argumento:

1. \( \log_{2}(1)\)

   Como el número \(1\) es la potencia \(2^0\),

   $$ \log_{2}(1) = \log_{2}(2^0) = 0 $$

2. \( \log_{2}(8)\)

   Como el número \(8\) es la potencia \(2^3\),

   $$ \log_{2}(8) = \log_{2}(2^3) = 3 $$

3. \( \log_{2}\left(\frac{1}{32}\right) \)

   El denominador es una potencia de \(2\):

   $$ \frac{1}{32} = \frac{1}{2^5} = 2^{-5}$$

   Por tanto,

   $$ \log_{2} \left(\frac{1}{32}\right) = \log_{2} (2^{-5}) = -5 $$

4. \( \log_{2}(0.25)\)

   Como el número decimal \(0.25\) es el resultado de la división \(1/4\) y esta fracción es \(2^{-2}\),

   $$ \log_{2}(0.25) = \log_{2} (2^{-2}) = -2 $$

5. \( \log_{2}(0.5)\)

   El número decimal \(0.25\) es la fracción \(1/2\), es decir, la potencia \(2^{-1}\). Por tanto,

   $$ \log_{2}(0.5) = \log_{2} (2^{-1}) = -1 $$

Ejercicio 3

Calculad los siguientes logaritmos (escribiendo los argumentos como potencias de la base del logaritmo):

1. \( \log_{3}(27)\)

2. \( \log_{5}(0.2)\)

3. \( \log_{6}(2^2\cdot 3^2)\)

4. \( \log_{7} \left( \frac{1}{49} \right) \)

5. \( \log_{9}(1)\)

Solución:

1. \( \log_{3}(27)\)

   Como \(27= 3^3\), el resultado es \(3\):

   $$ \log_{3}(27) = 3 $$

2. \( \log_{5}(0.2)\)

   Como \(0.2 = 1/5 = 5^{-1}\), el resultado es \(-1\):

   $$ \log_{5}(0.2) = -1 $$

3. \( \log_{6}(2^2\cdot 3^2)\)

   El argumento es \(36\) ya que

   $$ 2^2\cdot 3^2 = 4\cdot 9 = 36 $$

   Como \(36 =6^2\), el resultado es \(2\):

   $$ \log_{6}(2^2\cdot 3^2) = 2$$

4. \( \log_{7} \left( \frac{1}{49} \right) \)

   Como \(49 = 7^2\), la fracción es \(7^{-2}\) y el resultado del logaritmo es \(-2\):

   $$ \log_{7} \left( \frac{1}{49} \right) = -2 $$

5. \( \log_{9}(1)\)

   Como \(1 = 9^0\), el logaritmo es \(0\):

   $$ \log_{9}(1) = 0 $$

Ejercicio 4

Calcular el valor de la incógnita \(x\) de los argumentos para que el resultado del logaritmo sea el indicado:

1. \( \log_{e}( x+1 ) = 2\)

2. \( \log_{3}( x^3 ) = 3\)

3. \( \log_{5} ( x + 1 ) = 2 \)

4. \( \log_{10}( 3x +1 ) = 2\)

5. \( \log_{e}( 1 -2x ) = 5\)

Solución:

Antes de empezar, recordad que el logaritmo en base \(b\) de \(a\) es igual a \(c\) si \(b^c = a\).

Como nosotros conocemos \(b\) y \(c\), para calcular la incógnita \(x\) (que está en \(c\)) resolveremos la ecuación

$$ b^c = a $$

1. \( \log_{e}( x+1 ) = 2\)

   El logaritmo natural (base \(e\)) de \(x+1\) es \(2\) cuando

   $$ e^2 = x + 1 $$

   Por tanto, la incógnita \(x\) debe ser \(x = e^2-1\).

2. \( \log_{3}( x^3 ) = 3\)

   El logaritmo en base \(3\) de \(x^3\) es \(3\) cuando

   $$ 3^3 = x^3 $$

   Por tanto, la incógnita debe ser \(x = 3\).

3. \( \log_{5} ( x + 1 ) = 2 \)

   El logaritmo en base \(5\) de \(x+1\) es \(2\) cuando

   $$ 5^2 = x +1 $$

   Resolvemos la ecuación:

   $$ 25 = x +1 $$

   $$ 25 -1 = x $$

   $$ 24 = x $$

   Por tanto, la incógnita debe ser \(x = 24\).

4. \( \log_{10}( 3x +1 ) = 2\)

   Resolvemos la ecuación

   $$ 10^2 = 3x +1 $$

   $$ 100 = 3x +1 $$

   $$ 100-1 = 3x $$

   $$ 99 = 3x $$

   Recordad que el coeficiente \(3\) de la incógnita pasa dividiendo:

   $$ x = \frac{99}{3} = 33 $$

5. \( \log_{e}( 1 -2x ) = 5\)

   Resolvemos la ecuación

   $$ e^5 = 1-2x $$

   $$ 2x = 1 -e^5 $$

   El coeficiente \(2\) de la incógnita pasa dividiendo:

   $$ x = \frac{1-e^5}{2} $$

Problema 1

¿Por qué el logaritmo (en cualquier base) de \(1\) siempre es \(0\)?

$$ \log_b (1) = 0 $$

Solución:

En la definición del logaritmo (al comienzo de la página) dijimos que la base de un logaritmo tiene que ser un número positivo y distinto de \(1\):

$$ b > 0, b\neq 1 $$

Sabemos que la potencia con exponente \(0\) de cualquier número \(b\) es \(1\):

$$ b^0 = 1 $$

Por tanto, el logaritmo de \(1\) siempre es \(0\):

$$ \log_b (1) = \log_b (b^0) = 0 $$

Problema 2

¿Cuándo un logaritmo decimal tiene un resultado entre \(0\) y \(1\) ?

Ayuda: tened en cuenta los siguientes logaritmos:

$$ \log_{10} (1) = 0 $$

$$ \log_{10}(10) = 1 $$

Solución:

El logaritmo decimal toma valores entre \(0\) y \(1\) cuando su argumento está entre \(1\) y \(10\).

Por ejemplo, la raíz cuadrada de \(10\) es un número (irracional) entre \(1\) y \(10\):

$$ \sqrt{10} \approx 3.162$$

Recordad que una raíz puede escribirse como una potencia:

$$ \sqrt{10} = 10 ^{\frac{1}{2}} = 10^{0.5} $$

Por tanto, su logaritmo está entre \(0\) y \(1\):

$$ \log (\sqrt{10} ) = \log (10^{0.5}) = 0.5 $$

Problema 3

¿Cuándo un logaritmo en base \(b> 1\) tiene un valor entre \(0\) y \(1\) ?

Ayuda: tened en cuenta el problema anterior.

Solución:

En el problema anterior nos hicimos la misma pregunta pero con el logaritmo en base \(10\). Dijimos que el logaritmo toma un valor entre \(0\) y \(1\) cuando su argumento está entre \(1\) y \(10\).

Podemos extender este razonamiento para cualquier base \(b\):

El logaritmo en base \(b\) toma un valor entre \(0\) y \(1\) cuando su argumento está entre \(1\) y \(b\).

Ejemplos:

• \( \log_2 ( \sqrt{2}\approx 1.414 ) = \log_2 ( 2^{0.5} ) = 0.5 \)

• \( \log_5 ( \sqrt{5}\approx 2.236 ) = \log_5 ( 5^{0.5} ) = 0.5 \)

• \( \log_e ( \sqrt{e}\approx 1.649 ) = \log_e ( e^{0.5} ) = 0.5 \)

Problema 4

¿Cuándo un logaritmo decimal tiene resultado negativo? ¿Y si no es decimal?

Solución:

Recordad que el logaritmo decimal de una potencia de \(10\) con exponente negativo tiene resultado negativo. Por ejemplo,

$$ \log_{10} (10^{-1}) = -1 $$

$$ \log_{10} (10^{-2}) = -2 $$

$$ \log_{10} (10^{-3}) = -3 $$

Estos números tienen en común que son números que están entre \(0\) y \(1\):

$$ 10^{-1} = 0.1 $$

$$ 10^{-2} = 0.01 $$

$$ 10^{-3} = 0.001 $$

$$ 10^{-1.5} \approx 0.032 $$

Los logaritmos (en cualquier base \(b > 1\)) tienen resultado negativo cuando su argumento es un número entre \(0\) y \(1\).

Problema 5

Observad la gráfica del logaritmo decimal para deducir el resultado del logaritmo cuando su argumento se aproxima a 0.

Solución:

Observando la gráfica, cuanto más se aproxima el argumento a \(0\), el logaritmo decrece más. Es decir, tiende a menos infinito:

$$ \lim_{x\to 0} \log (x) = -\infty $$

Observad los siguientes logaritmos:

$$ \log_{10} (10^{-1}) = \log_{10} (0.1) = -1$$

$$ \log_{10} (10^{-2}) = \log_{10} (0.01) = -2 $$

$$ \log_{10} (10^{-3}) = \log_{10} (0.001) = -3 $$

$$ \log_{10} (10^{-100}) = \log_{10} (0.00…01) = -100 $$

Problema 6

Si \(a \leq b\), ¿son ciertas las siguientes relaciones? ¿Por qué?

$$ \log (a) \leq \log (b) $$

$$ \log_{5} (x) \leq \log_{3} (x), \forall x \geq 1 $$

Ayuda: observad las gráficas.

Solución:

La primera relación es cierta porque ya hemos visto en las gráficas que los logaritmos son funciones crecientes y, por tanto, cuando mayor es su argumento, mayor es su resultado.

También dijimos anteriormente que cuando mayor es la base \(b\) de un logaritmo, más pequeño es su resultado para el mismo argumento siempre que \( x \geq 1\). Así que la segunda relación también es cierta.