La función logaritmo
Esta página está dedicada a la función logaritmo \(f(x) = \log_b(x)\). Vamos a demostrar la continuidad, la derivabilidad y a calcular la derivada, la integral indefinida, la integral definida y la integral impropia.
Es imprescindible conocer las propiedades de los logaritmos y tener conocimientos básicos de cálculo diferencial y cálculo integral.
Nivel orientativo: preuniversitario.
Definición
Dado \(b\in\left]0, +\infty\right[ -\{ 1 \}\), la función logaritmo en base \(b\) es la función de variable real
$$ f_b: \mathbb{R}^+ \rightarrow \mathbb{R}$$
$$ f_b(x) = \log_b(x) $$
Nota: \(\mathbb{R}^+ := \left]0, +\infty\right[\) y \( \mathbb{R} := \left]-\infty, +\infty \right[ \).
Gráfica de la función para distintos valores de \(b\):
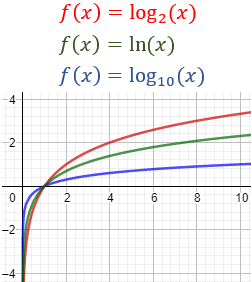
Dominio e imagen
El dominio de la función logaritmo (en cualquier base) es los reales positivos:
$$ Dom(f_b) =\mathbb{R}^+= \left]0, +\infty\right[ $$
Y su imagen (o recorrido) es todos los reales:
$$ Img(f_b) = \mathbb{R} = \left]-\infty, +\infty \right[ $$
Continuidad
La función logaritmo es continua en todo su dominio (independientemente de la base).
Demostración:
Vamos a hacer primero la demostración para el logaritmo natural (logaritmo con base \(e\approx 2.7183)\).
Sea \( a\in \left]0, +\infty\right[ \):
Dado \(\varepsilon > 0\), definimos
$$ \delta = a\cdot e^\varepsilon -a =$$
$$ = a\cdot (e^\varepsilon -1) > 0 $$
Si \(|x-a| < \delta\), entonces
$$ x-a < \delta $$
$$ x-a < a\cdot e^\varepsilon -a $$
$$ x < a\cdot e^\varepsilon $$
$$ \frac{x}{a} < e^\varepsilon $$
Como \( e^{\log_e (x/a)} = x/a\), entonces
$$ e^{\log_e (x/a)} < e^\varepsilon $$
Y como la base \(e\) es mayor que \(1\),
$$ \log_e \left( \frac{x}{a} \right) < \varepsilon $$
Finalmente,
$$ \varepsilon > \log_e \left( \frac{x}{a} \right) = |\log_e \left( \frac{x}{a} \right) | = $$
$$ = |\log_e(x) - \log_e (a) |$$
Por tanto, el logaritmo natural es continua para todo \( a\in \left]0, +\infty\right[ \).
Para demostrar la continuidad del logaritmo en cualquier base \(b \neq e\), tened en cuenta que
$$ \log_b (x) = \frac{\log_e (x) }{\log_e (b)} $$
Es decir, si \(K = 1/\log_e(b)\), entonces
$$ f_b(x) =\log_b (x) = K\cdot \log_e(x) $$
Como \(K\neq 0\) es constante y \( \log_e\) es continua, entonces \(f_b\) también es continua. Demostramos esto último:
Sea \( a\in \left]0, +\infty\right[ \):
Dado \(\varepsilon > 0\), definimos
$$ {\varepsilon}_0 = \frac{\varepsilon}{|K|} > 0$$
Como \( {\varepsilon }_0 > 0\) y la función logaritmo natural es continua en \(a\), existe \(\delta > 0\) tal que si \( |x-a| < 0\), entonces
$$ |\log_e (x) - \log_e (a)| < {\varepsilon}_0 $$
Veamos que se cumple la condición de continuidad del logaritmo en base \(b\):
$$ |\log_b(x) -\log_b(a)| =$$
$$ = |K\cdot \log_e(x) -K\cdot \log_e(a)| =$$
$$ = |K|\cdot |\log_e(x) -\log_e(a)| < |K|\cdot {\varepsilon}_0 = \varepsilon $$
Función inversa
La función inversa de la función logaritmo en base \(b\) es la función
$$ f^{-1}_b: \mathbb{R} \rightarrow \mathbb{R}^+$$
$$ f^{-1}_b(x) = b^x $$
Gráfica de la función inversa para distintos valores de \(b\):
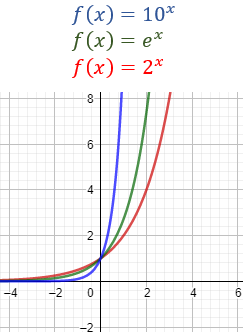
Demostración:
La demostración es muy simple ya que sólo tenemos que comprobar que la composición de las funciones es la función identidad en los respectivos dominios.
Calculamos \(f_b \circ f^{-1}_b\):
$$ f_b \left( f^{-1}_b (x) \right) = f_b ( b^x ) = $$
$$ = \log_b (b^x) = x $$
Calculamos \(f^{-1}_b \circ f_b\):
$$ f^{-1}_b \left( f_b (x) \right) = f^{-1}_b (\log_b(x) ) = $$
$$ = b^{\log_b (x)} = x $$
En adelante escribiremos el logaritmo natural (logaritmo en base \(e\)) de \(x\) como \( \ln (x)\).
Derivabilidad
La función logaritmo es derivable en su dominio y su derivada es
$$ \frac{\partial }{\partial x} \log_b (x) = \frac{1}{x\cdot \ln(b)} $$
Y en particular, la derivada del logaritmo natural es
$$ \frac{\partial }{\partial x} \ln (x) = \frac{1}{x} $$
Demostración:
Recordad que una función \(f\) es derivable en el punto \(a\) de su dominio si existe el límite
$$ \lim_{h\to 0} \frac{f(a+h)-f(a)}{h} = \frac{\partial }{\partial x} f(a) = f'(a)$$
En lugar de estudiar la derivabilidad en el punto \(a\) lo haremos para todo \(x\) del dominio de la función logaritmo en base \(b\).
Antes de calcular el límite, vamos a reescribir la fracción:
$$ \frac{ \log_b(x+h) -\log_b(x) }{ h } = $$
$$ = \frac{ \log_b \left( \frac{x+h}{x}\right) }{ h } = $$
$$ = \log_b \left( \frac{x+h}{x}\right)^\frac{1}{h} = $$
$$ = \log_b \left( 1+\frac{h}{x}\right)^\frac{1}{h} = $$
$$ = \log_b \left( \left( 1+\frac{h}{x}\right)^\frac{1}{h} \right)^\frac{x}{x} = $$
$$ = \log_b \left( \left( 1+\frac{h}{x}\right)^\frac{x}{h} \right)^\frac{1}{x} = $$
$$ = \frac{1}{x} \cdot \log_b \left( 1+\frac{h}{x}\right)^\frac{x}{h} = $$
$$ = \frac{1}{x} \cdot \log_b \left( 1+\frac{1}{\frac{x}{h}}\right)^\frac{x}{h} = $$
Observad que el límite del argumento del logaritmo anterior es el número \(e\), así que el límite que queremos calcular es
$$ \frac{\partial }{\partial x} \log_b (x) =$$
$$ = \lim_{h\to 0} \frac{ \log_b(x+h) -\log_b(x) }{ h } = $$
$$ = \frac{1}{x}\cdot \log_b (e) $$
Si cambiamos a logaritmo natural,
$$ \frac{\partial }{\partial x} \log_b (x) = \frac{1}{x}\cdot \frac{\ln (e) }{\ln (b) } =$$
$$ = \frac{1}{x\cdot \ln(b)} $$
Como consecuencia, la derivada del logaritmo natural (\(b = e\)) es
$$ \frac{\partial }{\partial x} \ln (x) = \frac{1}{x} $$
Primitivas
$$ \int{ \log_b(x) }dx = x\cdot \frac{\ln(x)-1}{\ln(b)}+K,$$
$$ K\in\mathbb{R}$$
Demostración:
Aplicamos integración por partes:
$$ \int{udv} = u\cdot v -\int{vdu} $$
Llamamos \(u = \log_b (x) \) y \(dv = 1\). Entonces,
$$ du = \frac{1}{ x\cdot \ln(b) } dx$$
$$ v = x $$
Por tanto,
$$ \int{ \log_b(x) }dx =$$
$$= x\cdot \log_b (x) -\int{ \frac{x}{ x\cdot \ln(b) }}dx = $$
$$ = x\cdot \log_b (x) -\int{ \frac{1}{ \ln(b) }}dx =$$
$$ = x\cdot \log_b (x) -\frac{1}{ \ln(b) } \cdot \int{ 1}dx =$$
$$ = x\cdot \log_b (x) -\frac{x}{ \ln(b) } + K=$$
$$ = x\cdot \left( \log_b (x) -\frac{1}{ \ln(b) } \right) + K=$$
$$ = x\cdot \left( \frac{\ln (x)}{\ln(b)} -\frac{1}{ \ln(b) } \right) + K=$$
$$ = x\cdot \left( \frac{\ln (x) - 1}{\ln(b)} \right) + K$$
Integral definida
$$ \int_{A}^B \log_b(x)dx = \frac{ \ln \left( \frac{B^B}{A^A} \right) +A -B }{\ln(b)} $$
Demostración:
Sean \(A> B > 0 \), teniendo en cuenta el apartado anterior y aplicando la regla de Barrow:
$$ \int_{A}^B \log_b(x)dx = $$
$$= B \cdot \frac{\ln(B)-1}{\ln(b)} - A \cdot \frac{\ln(A)-1}{\ln(b)} = $$
$$ = \frac{1}{\ln(b)} \cdot \left( B\ln(B)-B -A\ln(A)+A \right)=$$
$$ = \frac{1}{\ln(b)} \cdot \left( \ln(B^B)-B -\ln(A^A)+A \right)=$$
$$ = \frac{1}{\ln(b)} \left( \ln \left( \frac{B^B}{A^A} \right) +A -B\right)$$
Integral impropia
$$ \int_{0}^B \log_b(x)dx = \frac{ \ln \left( B^B \right) -B }{\ln(b)},\ B > 0$$
Nota: la integral \( \int_{A}^{+\infty} \log_b(x)dx\) no converge.
Demostración:
Teniendo en cuenta el apartado anterior,
$$ \int_{0}^B \log_b(x)dx = $$
$$ =\lim_{A\to 0} \int_{A}^B \log_b(x)dx =$$
$$ =\lim_{A\to 0} \frac{ B\ln(B)-B -A\ln(A)+A }{\ln(b)} =$$
$$ = \frac{ B\ln(B)-B }{\ln(b)} =$$
$$ = \frac{ \ln \left( B^B \right) -B }{\ln(b)} $$
Nota: en el cálculo del límite hemos tenido en cuenta que
$$ \lim_{A\to 0} A\cdot \ln(A) = 0$$
Este último límite es fácil de calcular aplicando la regla de L'Hôpital.